Utopia: Model of Flocking Dynamics

SimpleFlocking

Model of Flocking Dynamics

The SimpleFlocking agent-based model implements one of the earliest models of collective dynamics that shows a phase transition. It was proposed by Viczek et al. in 1995 and is inspired by the swarm behavior of schools of fish or flocks of birds (hence the name).

Agents in the so-called `flocking` configuration

Results from the `noise_sweep`, showing the effect of orientational noise.

Agents at the onset of self-organized flocking (left) and the effect of orientational noise on the coherence of collective movement (right). (click to enlarge)

Fundamentals

Each agent in the SimpleFlocking model is characterized by its position in space, its orientation, and a (constant) speed.

The model mechanisms are very simple: In each time step, …

… all agents' orientations are adjusted to the mean value of those agents within an interaction radius (including the agent itself), plus some angular noise.
… all agents' positions are updated using the displacement vector that results from the change in orientation. These updates occur synchronously for all agents. Implementation Details

Observables

agent: group that contains agent-specific data, labelled by time and agent id
- x and y: agent position
- orientation: agent orientation in radians [−π, +π]
norm_group_velocity: the normalized average group velocity time series. This is what Vicsek et al., 1995, refer to as the order parameter of the system.
orientation_circmean: circular mean orientation time series
orientation_circstd: circular standard deviation of orientation time series

Note the need for circular statistics in order to allow calculating these observables.

Configuration Sets

The following configuration sets aim to reproduce some of the results of the Vicsek et al., 1995, paper. The parameters are those used in the referenced figures in that paper.

flocking: A scenario where the agents show flocking behavior (Figure 1b).
ordered: A scenario leading to a globally ordered movement (Figure 1d).
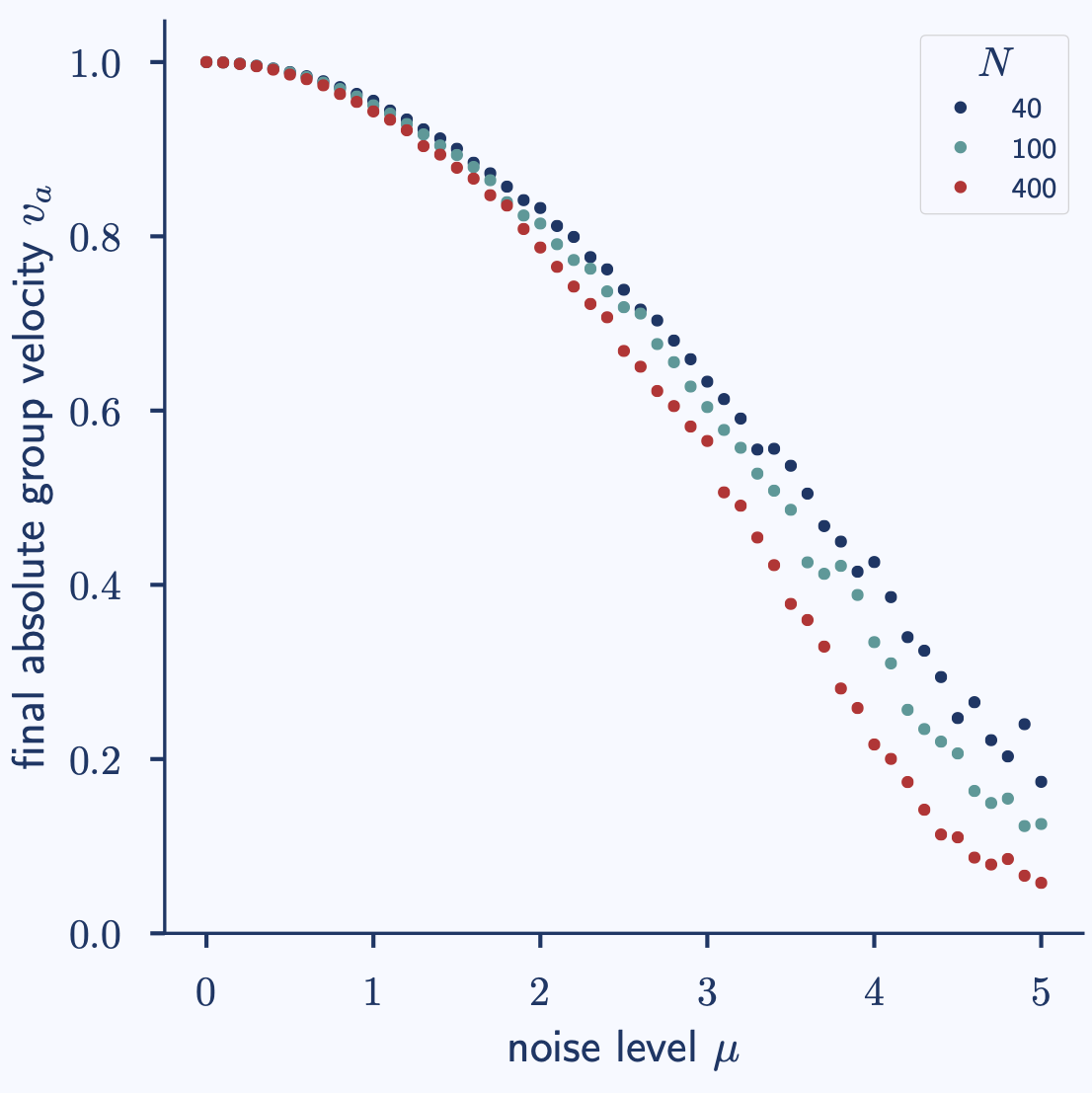
noise_sweep: A sweep that aims to reproduce Figure 2a: the order parameter over the system’s noise amplitude for different system sizes.
density_sweep: A sweep that aims to reproduce Figure 2b: the order parameter over the agent density.
The config sets with sweeps also include the corresponding plot configurations to generate the relevant figure.

Plots

The following general plots are available for the SimpleFlocking model:

agents_in_domain: shows the agents with color-coded orientation moving in the domain
time_series:
- norm_group_velocity: The normalized group velocity time series, which is used as the order parameter by Vicsek et al..
- orientation_circstd: The circular standard deviation of the agents’ orientation over time, which can also be interpreted as an order parameter.
- orientation: A combined plot of the circular mean and circular standard deviation of the agent orientation over time.

For details on how to further configure these, see the plot configurations.